PBR(物理ベースレンダリング)の理論

https://learnopengl.com/PBR/Theory

PBR、またはより一般的には 物理ベースのレンダリングは、多かれ少なかれ物理的な世界の理論とより密接に一致する同じ基本的な理論に基づいたレンダリング手法のコレクションです。物理ベースのレンダリングは、物理的にもっともらしい方法で光を模倣することを目的としているため、PhongやBlinn-Phongなどのオリジナルの照明アルゴリズムと比較して、より現実的に見えます。見た目がよくなるだけでなく、実際の物理に非常に近いため、照明を正しく見せるために安価なハックや微調整に頼ることなく、物理パラメータに基づいてサーフェスマテリアルを作成できます。物理パラメータに基づいてマテリアルを作成することの大きな利点の1つは、これらのマテリアルが照明条件に関係なく正しく見えることです。非PBRパイプラインには当てはまらないもの。

物理ベースのレンダリングは、それでも（物理学の原理に基づいた）現実の近似です。そのため、物理シェーディングではなく、物理ベースのシェーディングと呼ばれています。PBRライティングモデルが物理ベースと見なされるためには、次の3つの条件を満たしている必要があります（心配しないでください。すぐに対応します）。

  1. マイクロファセットサーフェスモデルに基づいている。

  2. エネルギーを節約します。

  3. 物理ベースのBRDFを使用します。

次のPBRの章では、最初にディズニーが探索し、Epic Gamesがリアルタイム表示に採用したPBRアプローチに焦点を当てます。に基づく彼らのアプローチメタリックワークフロー、きちんと文書化されており、ほとんどの人気のあるエンジンに広く採用されており、見た目もすばらしく見えます。これらの章の終わりまでに、次のようなものになります。

これらの章のトピックはかなり進んでいるため、OpenGLとシェーダーライティングを十分に理解することをお勧めします。このシリーズに必要なより高度な知識には、フレームバッファ、キューブマップ、ガンマ補正、HDR、法線マッピングがあります。また、いくつかの高度な数学についても掘り下げますが、概念をできるだけ明確に説明できるように最善を尽くします。

マイクロファセットモデル

すべてのPBR技術は、マイクロファセットの理論に基づいています。理論は、微視的スケールのどの表面も、マイクロファセット。表面の粗さに応じて、これらの小さな小さなミラーの配置はかなり大きく異なります。

表面が粗くなるほど、各マイクロファセットは表面に沿って無秩序に整列します。これらの小さな鏡のような配置の効果は、鏡面反射照明/反射について具体的に述べると、入射光線が散らすより粗い表面で完全に異なる方向に沿って、より広範囲の鏡面反射をもたらします。対照的に、滑らかな表面では、光線はほぼ同じ方向に反射する可能性が高く、反射が小さく鋭くなります。

微視的なレベルでは完全に滑らかな表面はありませんが、これらのマイクロファセットはピクセルごとに区別できないほど小さいので、与えられた表面のマイクロファセットの粗さを統計的に概算します 粗さパラメータ。表面の粗さに基づいて、いくつかのベクトルに大まかに整列したマイクロファセットの比率を計算できますhh。このベクトルhh それは 途中ベクトル それは光の中間に座っています ll そして見る vvベクター。前に、次の合計として計算される高度な照明の章で中間ベクトルについて説明しましたll そして vv その長さで割った：

マイクロファセットが中間ベクトルに整列するほど、鏡面反射がよりシャープで強力になります。0と1の間で変化する粗さパラメーターと共に、マイクロファセットの配置を統計的に概算できます。

粗さの値が大きいほど、鏡面反射の形状が大きくなり、滑らかな表面の鏡面反射の形状が小さくて鋭いのとは対照的です。

エネルギー資源の保護

マイクロファセットの近似では、 エネルギー資源の保護：出射光エネルギーが入射光エネルギーを超えてはなりません（放射面を除く）。上の画像を見ると、鏡面反射領域が増加していますが、粗さのレベルを上げるとその輝度も減少しています。鏡面反射強度が各ピクセルで同じである場合（鏡面反射形状のサイズに関係なく）、粗い表面ははるかに多くのエネルギーを放出し、エネルギー保存の原則に違反します。これが、滑らかな表面では鏡面反射がより強く、粗い表面ではより暗く見える理由です。

省エネを維持するには、拡散光と鏡面反射光を明確に区別する必要があります。光線が表面に当たった瞬間、それは両方に分割されます屈折 一部と 反射部。反射部分は、直接反射して表面に進入しない光です。これが鏡面照明として知られています。屈折部分は、表面に入射して吸収される残りの光です。これは、拡散照明と呼ばれるものです。

屈折した光は表面に触れてもすぐには吸収されないため、ここにはいくつかのニュアンスがあります。物理学から、光はすべてのエネルギーを失うまで前進し続けるエネルギーのビームとしてモデル化できることがわかっています。光ビームがエネルギーを失う方法は、衝突によるものです。各マテリアルは、次の図に示すように、光線と衝突する可能性のある小さな粒子で構成されています。粒子は、衝突のたびに光のエネルギーの一部または全部を吸収し、熱に変換されます。

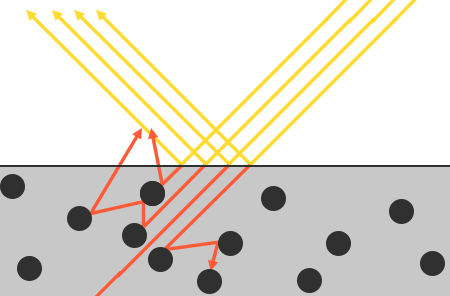
一般に、すべてのエネルギーが吸収されるわけではなく、光は継続します 散らす（ほとんど）ランダムな方向で、エネルギーが枯渇するか、再び表面から離れるまで、他の粒子と衝突します。表面から再び出現する光線は、表面の観察された（拡散）色に寄与します。ただし、物理ベースのレンダリングでは、屈折したすべての光が非常に小さな衝撃領域で吸収および散乱され、距離を置いて表面から出る散乱光線の影響を無視するという簡単な仮定をします。これを考慮した特定のシェーダー技術は、表面下散乱 肌、大理石、ワックスなどの素材の視覚的品質を大幅に向上させるが、パフォーマンスを犠牲にするテクニック。

反射と屈折に関してさらに微妙なのは、 メタリック。金属表面は、非金属表面（別名、誘電体）。金属表面は反射と屈折の同じ原理に従いますが、すべての屈折した光は散乱することなく直接吸収されます。つまり、金属表面は反射光または鏡面反射光のみを残します。金属表面は拡散色を示しません。この金属と誘電体の明確な違いにより、PBRパイプラインではどちらも異なる扱いがされているため、この章でさらに詳しく説明します。

反射光と屈折光のこの区別により、エネルギー保存に関する別の観察結果が得られます。これらは相互に排他的です。反射された光エネルギーは、素材自体に吸収されなくなります。したがって、屈折した光として表面に入射するために残されたエネルギーは、反射を考慮に入れた後の結果として生じるエネルギーです。

入射光のエネルギーが反射される割合を表す鏡面反射率を最初に計算することにより、このエネルギー保存関係を保存します。屈折した光の割合は、次のように鏡面反射率から直接計算されます。

float kS = calculateSpecularComponent(…); // reflection/specular fractionfloat kD = 1.0 – kS; // refraction/diffuse fraction

このようにして、エネルギー保存の原則に従って、入射光が反射する量と屈折する量の両方がわかります。このアプローチでは、屈折/拡散と反射/鏡面の両方の寄与を超えることは不可能であるため1.0、それらのエネルギーの合計が入射光エネルギーを超えないようにします。以前の照明の章で考慮していなかったこと。

反射方程式

これにより、レンダー方程式と呼ばれるものがあります。これは、非常に賢い人々が考え出した精巧な方程式で、現在、光の視覚をシミュレートするのに最適なモデルです。物理ベースのレンダリングは、レンダー方程式のより特殊なバージョンに強く従います。反射方程式。PBRを適切に理解するには、まず反射率方程式をしっかりと理解することが重要です。

反射率の方程式は最初は気が遠くなるように見えますが、これから分析していくと、ゆっくりと理解し始めます。方程式を理解するには、少し詳しく調べなければなりません放射測定。放射測定は、可視光を含む電磁放射の測定です。表面および方向の光を測定するために使用できる放射測定量はいくつかありますが、ここでは、次のように知られている反射方程式に関連する1つの放射測定量についてのみ説明します。輝き、ここでは LL。放射輝度は、単一方向からの光の大きさまたは強さを定量化するために使用されます。放射輝度は複数の物理量の組み合わせであるため、最初に理解するのは少し難しいので、最初にそれらに焦点を当てます。

放射束：放射束ΦΦワットで測定された光源の透過エネルギーです。光は、複数の異なる波長にわたるエネルギーの総和であり、各波長は特定の（可視）色に関連付けられています。したがって、光源の放出エネルギーは、そのすべての異なる波長の関数として考えることができます。390nmから700nm（ナノメートル）の間の波長は、可視光スペクトルの一部、つまり人間の目で認識できる波長と見なされます。以下は、昼光の波長ごとのさまざまなエネルギーの画像です。

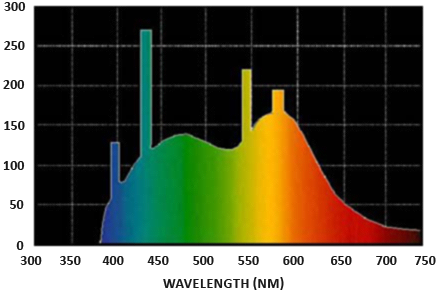
放射束は、異なる波長のこの関数の総面積を測定します。この波長の測定値を入力として直接取るのは少し実用的ではないため、放射束をさまざまな波長強度の関数としてではなく、RGB（または一般にそれと呼ばれるように）エンコードされた明るい色のトリプレットとして表すことを単純化することがよくあります。色）。このエンコードでは情報がかなり失われますが、視覚的な側面では一般に無視できます。

立体角：次のように表される立体角ωω、単位球に投影された形状のサイズまたは面積を示します。この単位球に投影された形状の領域は、立体角; 立体角をボリュームのある方向として視覚化できます。

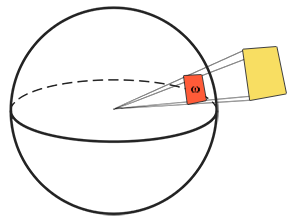
この単位球の中心にいる観察者であり、形状の方向を見ていると考えてください。シルエットの大きさは立体角です。

放射強度：放射強度は、立体角あたりの放射束の量、または単位球への投影面積に対する光源の強度を測定します。たとえば、全方向に均等に放射する全方向性の光が与えられた場合、放射強度は特定の領域（立体角）にエネルギーを与えることができます。

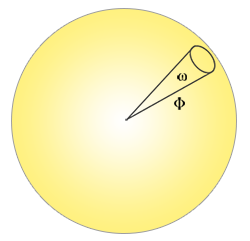
放射強度を表す式は次のように定義されます。

私=dΦdω私=dΦdω

どこ 私私 放射束です ΦΦ 立体角を超えて ωω。

放射束、放射強度、立体角の知識があれば、最後に放射輝度の方程式を記述できます。放射輝度は、エリアで観測されたエネルギーの合計として記述されますああ 立体角を超えて ωω 放射強度の光の ΦΦ：

L =d2ΦdA dω COSθL=d2Φdあdωcos⁡θ

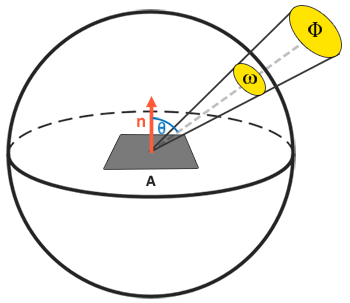
放射輝度は、エリア内の光の量の放射測定であり、 インシデント （または入力）角度 θθ 表面の法線への光の cosθcos⁡θ：表面に直接放射される光が少ないほど光は弱く、表面に直接垂直であるときに光が最も強くなります。これは、基本的な照明の章からの拡散照明の知覚に似ています。cosθcos⁡θ ライトの方向ベクトルと表面法線の間の内積に直接対応します。

float cosTheta = dot(lightDir, N);

放射輝度方程式は、対象となるほとんどの物理量を含んでいるため、非常に便利です。立体角を考えると ωω とエリア ああ無限に小さくするには、放射輝度を使用して、空間内の単一の点に当たる単一の光線のフラックスを測定できます。この関係により、単一の（フラグメント）ポイントに影響を与える単一の光線の輝度を計算できます。立体角を効果的に変換しますωω 方向ベクトルに ωω、および ああ ポイントに pp。このようにして、シェーダーの放射輝度を直接使用して、単一の光線のフラグメントごとの寄与を計算できます。

実際に、それが輝きになると、私たちは一般的に点に入射するすべての光を気にしますppとして知られているすべての輝きの合計です 放射照度。放射輝度と放射輝度の両方の知識があれば、反射方程式に戻ることができます。

私たちは今それを知っています LL レンダリング方程式のある点の輝度を表します pp 入ってくる無限に小さい立体角 ω私ω私 入力方向ベクトルと考えることができます ω私ω私。覚えてcosθcos⁡θ 表面への光の入射角に基づいてエネルギーをスケーリングします。これは、反射方程式で次のようにわかります。 反射方程式は、反射された放射輝度の合計を計算しますoポイントの pp 方向に ωoωoこれは、視聴者への発信方向です。または別の言い方をすると：LoLo ポイントへのライトの放射照度の反射合計を測定します pp から見た ωoωo。

反射率の式は放射照度に基づいています。これは、光を測定するすべての入射放射照度の合計です。単一の入射光方向だけでなく、半球内のすべての入射光方向ΩΩ ポイントを中心に pp。あ半球 表面の法線の周りに配置された半分の球として説明できます んん：

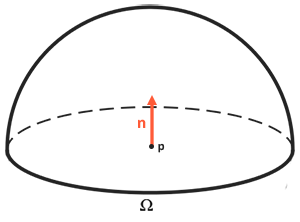
領域または（半球の場合は）ボリューム内の値の合計を計算するには、 積分 反射方程式で次のように表されます ∫∫ すべての着信方向 dω私dω私 半球内 ΩΩ。積分は関数の面積を測定し、分析的または数値的に計算できます。レンダリング方程式と反射方程式の両方に対する解析解はないため、積分を離散的に数値的に解決する必要があります。これは、半球全体の反射率方程式の小さな離散ステップの結果を取得することになります。ΩΩそして、ステップサイズで結果を平均化します。これは、リーマン和 おおよそ次のようにコードで視覚化できます。

int steps = 100;

float sum = 0.0f;

vec3 P = …;

vec3 Wo = …;

vec3 N = …;

float dW = 1.0f / steps;

for(int i = 0; i < steps; ++i)

{

vec3 Wi = getNextIncomingLightDir(i);

sum += Fr(P, Wi, Wo) * L(P, Wi) * dot(N, Wi) * dW;

}

ステップをdWでスケーリングすると、合計は積分関数の総面積または体積に等しくなります。dW各離散ステップをスケーリングすると考えることができますdω私dω私反射方程式で。数学的にdω私dω私これは、積分を計算するための連続的なシンボルでありdW、コードでは直接関係しませんが（これはリーマン和の離散ステップであるため）、このように考えると役立ちます。個別のステップを実行すると、常に関数の総面積の概算が得られることに注意してください。注意深く読むと、ステップ数を増やすことでリーマン和の精度を上げることができることに気付くでしょう。

反射方程式は、すべての入射光方向の放射輝度を合計します ω私ω私 半球以上 ΩΩ スケーリング frfr そのヒットポイント pp 反射光の合計を返します LoLo視聴者の方向に。入ってくる放射輝度は、慣れている光源から、またはIBLの章で説明するように、すべての入ってくる方向の放射輝度を測定する環境マップから取得できます。

今、唯一の未知の左は frfr として知られているシンボル BRDF または 双方向反射分布関数 サーフェスのマテリアルプロパティに基づいて、入ってくる放射輝度をスケーリングまたは重み付けします。

BRDF

の BRDF、または 双方向反射分布関数は、入力（光）方向を入力として受け取る関数です。 ω私ω私、発信（ビュー）方向 ωoωo、表面法線 んん、および表面パラメータ aaこれは、マイクロサーフェスの粗さを表します。BRDFは、個々の光線の量を概算しますω私ω私その材料特性を考慮して、不透明な表面の最終反射光に寄与します。たとえば、表面が完全に滑らかな表面を持っている場合（ミラーのようなもの）、BRDF関数はすべての入射光線に対して0.0を返しますω私ω私 出射光線と同じ（反射）角度を持つ1つの光線を除く ωoωo 関数が1.0を返す点。

BRDFは、前述のマイクロファセット理論に基づいて、材料の反射および屈折特性を近似します。BRDFを物理的にもっともらしくするには、エネルギー保存の法則を尊重する必要があります。つまり、反射光の合計が入射光の量を超えてはなりません。技術的には、Blinn-PhongはBRDFと同じと見なされていますω私ω私 そして ωoωo入力として。ただし、ブリンフォンは省エネの原則に準拠していないため、物理ベースとは見なされません。光に対する表面の反応を概算するために、物理ベースのBRDFがいくつかあります。ただし、ほとんどすべてのリアルタイムPBRレンダーパイプラインは、クックトーランスBRDF。

Cook-Torrance BRDFには、拡散部分と鏡面部分の両方が含まれています。

入射光エネルギーの前述の比であり、屈折とksks反映される比率です。BRDFの左側は、ここで示される方程式の拡散部分を示します。これはランベルト拡散 拡散シェーディングに使用したものに似ています。これは、次のように示される定数係数です。

と アルベドまたは表面色（拡散表面テクスチャと考えてください）。BRDFを含む先に示した積分が次のようにスケーリングされるため、拡散光を正規化するためにpiによる除算がありますππ（これについては、IBLの章で説明します）。

このランバートディフューズが、これまで使用してきたディフューズライティングとどのように関係しているのか不思議に思うかもしれません。サーフェスの色に、サーフェスの法線と光の方向の間の内積を掛けたものです。ドット積はまだありますが、BRDFから移動しました。

BRDFの拡散部分にはさまざまな方程式が存在しますが、より現実的に見える傾向がありますが、計算コストも高くなります。しかし、エピックゲームズによって結論付けられているように、ランバートの拡散は、ほとんどのリアルタイムレンダリングの目的には十分です。

BRDFのスペキュラ部分は少し高度であり、次のように説明されます。

Cook-TorranceスペキュラーBRDFは、3つの関数と分母の正規化係数で構成されています。D、F、Gの各シンボルは、表面の反射特性の特定の部分を近似する関数のタイプを表します。これらは、通常のD分布関数、Fレスネル方程式、およびG幾何学関数として定義されます。

  • 正規分布関数：表面の粗さの影響を受けて、表面のマイクロファセットが中間ベクトルに整列する量を概算します。これは、マイクロファセットを近似する主要な機能です。

  • ジオメトリ関数：マイクロファセットのセルフシャドウプロパティを記述します。表面が比較的粗い場合、表面のマイクロファセットが他のマイクロファセットを覆い隠して、表面が反射する光を減らすことができます。

  • フレネル方程式：フレネル方程式は、さまざまな表面角度での表面反射の比率を表します。

これらの関数のそれぞれは、同等の物理学の近似であり、基礎となる物理学をさまざまな方法で近似することを目的としたそれぞれのバージョンが複数見つかります。より現実的なものもあれば、より効率的なものもあります。使用するこれらの関数の近似バージョンを選択することは完全に問題ありません。Epic GamesのBrian Karisは、ここで複数のタイプの近似について多くの研究を行いました。Epic GameのUnreal Engine 4で使用されているのと同じ関数を選択します。DにはTrowbridge-Reitz GGX、FにはFresnel-Schlick近似、GにはSmithのSchlick-GGXを使用します。

正規分布関数

の 正規分布関数 DD （中間）ベクトルに正確に整列したマイクロファセットの相対表面積を統計的に概算します hh。いくつかの粗さパラメーターが与えられた場合にマイクロファセットの一般的な配置を統計的に概算する多数のNDFがあり、使用するものはTrowbridge-Reitz GGXとして知られています。

ここに hh は、表面のマイクロファセットに対して測定する中間ベクトルです。 aa表面の粗さの尺度です。取るならhh さまざまな粗さパラメーターでの表面の法線と光の方向の間の中間ベクトルとして、次の視覚的な結果が得られます。

粗さが低い（したがって表面が滑らかである）場合、非常に集中した数のマイクロファセットが小さな半径の中間ベクトルに整列します。この高濃度のため、NDFは非常に明るいスポットを表示します。しかし、粗い表面では、マイクロファセットがはるかにランダムな方向に整列しているため、はるかに多数の中間ベクトルが見つかりますhh マイクロファセットにいくらか整列しますが、濃度は低くなりますが、より灰色がかった結果が得られます。

GLSLでは、Trowbridge-Reitz GGX正規分布関数は次のコードに変換されます。

float DistributionGGX(vec3 N, vec3 H, float a)

{

float a2 = a*a;

float NdotH = max(dot(N, H), 0.0);

float NdotH2 = NdotH*NdotH;

float nom = a2;

float denom = (NdotH2 * (a2 – 1.0) + 1.0);

denom = PI * denom * denom;

return nom / denom;

}

ジオメトリ関数

ジオメトリ関数は、相対的な表面積を統計的に概算し、その微小な表面の細部が互いに影を落とし、光線が遮られます。

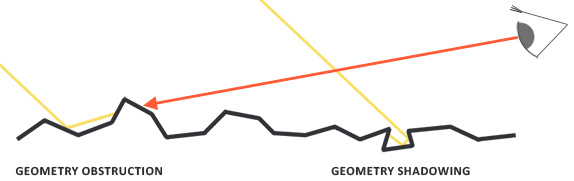
NDFと同様に、Geometry関数は、材料の粗さパラメーターを入力として受け取り、マイクロファセットを覆い隠す可能性が高い粗い表面を使用します。使用するジオメトリ関数は、GGXとSchlick-GGXとして知られるSchlick-Beckmann近似の組み合わせです。

ここに kk の再マッピングです αα 直接照明またはIBL照明のどちらにジオメトリ関数を使用しているかに基づいて：

の値に注意してください αα エンジンがラフネスをどのように変換するかによって異なる場合があります αα。次の章では、この再マッピングがどのように、どこで重要になるかを詳しく説明します。

ジオメトリを効果的に近似するには、ビューの方向（ジオメトリの障害物）と光の方向ベクトル（ジオメトリのシャドウイング）の両方を考慮する必要があります。両方を考慮に入れることができますスミスの方法：

 

Schlick-GGXでのSmithの方法の使用あなたbさまざまな粗さで次のような外観になりますR。

ジオメトリ関数は、[0.0、1.0]の乗数で、1.0（または白）はマイクロファセットシャドウイングを測定せず、0.0（または黒）は完全なマイクロファセットシャドウイングを測定します。

GLSLでは、geometry関数は次のコードに変換されます。

float GeometrySchlickGGX(float NdotV, float k)

{

float nom = NdotV;

float denom = NdotV * (1.0 – k) + k;

return nom / denom;

}

float GeometrySmith(vec3 N, vec3 V, vec3 L, float k)

{

float NdotV = max(dot(N, V), 0.0);

float NdotL = max(dot(N, L), 0.0);

float ggx1 = GeometrySchlickGGX(NdotV, k);

float ggx2 = GeometrySchlickGGX(NdotL, k);

return ggx1 * ggx2;

}

フレネル方程式

フレネル方程式（フレネルと発音）は、屈折する光に対して反射される光の比率を表します。これは、表面を見ている角度によって変化します。表面から視野への角度に基づいて、光が表面に当たった瞬間、フレネル方程式は反射される光の割合を示します。この反射率とエネルギー保存の原理から、光の屈折部分を直接得ることができます。

すべての表面または材料には、 ベース反射率表面を真っ直ぐ見た場合、角度を付けて表面を見た場合、すべての反射は表面の基本反射率と比較してよりはっきりします。これを確認するには、垂直の視野角から特定のレベルの基本反射率がある（おそらく）木製/金属の机を見てください。ただし、ほぼ90度の角度から机を見ると、反射が見えるようになります。はるかに明白です。完全な90度の角度から見た場合、すべての表面は理論的には完全に光を反射します。この現象は、フレネル フレネル方程式で記述されます。

フレネル方程式はかなり複雑な方程式ですが、幸運にもフレネル方程式は フレネルシュリック 近似：

0F0表面の基本反射率を表します。これは、屈折率またはIOR と呼ばれるものを使用して計算します。球体の表面に見られるように、表面のすれすれの角度（中間ビューの角度が90度に達している）に近づくほど、フレネルが強くなり、したがって反射が強くなります。

フレネル方程式にはいくつかの微妙な点があります。1つは、フレネルシュリック近似が実際に定義されるのは誘電または非金属表面。ために導体表面（金属）、屈折率を使用して基本反射率を計算することは適切に保持されず、導体に対して異なるフレネル方程式を使用する必要があります。これは不便なので、次のように表面の応答を事前計算してさらに近似します。通常発生 （F0F0）サーフェスを直接見ているかのように0度の角度で。金属と非金属の両方に同じ式を使用できるように、フレネルシュリック近似に従って、ビュー角度に基づいてこの値を補間します。

垂直入射での表面の応答、または基本反射率は、Naty Hoffmanのコースノートから取られた、以下にリストされているより一般的な値のいくつかを含むこれらのような大規模なデータベースで見つけることができます。

素材
F0F0 （線形）
F0F0 （sRGB）
色
水
(0.02, 0.02, 0.02)
 (0.15, 0.15, 0.15)  
プラスチック/ガラス（低）
(0.03, 0.03, 0.03)
(0.21, 0.21, 0.21)
プラスチック高
(0.05, 0.05, 0.05)
(0.24, 0.24, 0.24)
ガラス（高）/ルビー
(0.08, 0.08, 0.08)
(0.31, 0.31, 0.31)
ダイヤモンド
(0.17, 0.17, 0.17)
(0.45, 0.45, 0.45)
鉄
(0.56, 0.57, 0.58)
(0.77, 0.78, 0.78)
銅
(0.95, 0.64, 0.54)
(0.98, 0.82, 0.76)
ゴールド
(1.00, 0.71, 0.29)
(1.00, 0.86, 0.57)
アルミニウム
(0.91, 0.92, 0.92)
(0.96, 0.96, 0.97)
銀
(0.95, 0.93, 0.88)
(0.98, 0.97, 0.95)

ここで興味深いのは、すべての誘電体表面で、基本反射率が規則ではなく例外である0.17を超えないことです。一方、導体では、基本反射率が非常に高くなり、（ほとんどの場合）0.5と1.0の間で変化します。さらに、導体（または金属表面）の場合、ベースの反射率が薄くなります。これが理由ですF0F0RGBトリプレットとして表示されます（垂直入射での反射率は波長ごとに異なります）; これは、金属表面でのみ見られるものです。

誘電体表面と比較した金属表面のこれらの特定の属性により、 メタリックワークフロー。メタリックワークフローでは、次のように知られる追加のパラメーターを使用して、表面マテリアルを作成します。金属性 表面が金属表面か非金属表面かを示します。

理論的には、材料の金属性は二元的です。それは金属かそうでないかのどちらかです。両方にすることはできません。ただし、ほとんどのレンダーパイプラインでは、サーフェスのメタルネスを0.0〜1.0の間で直線的に構成できます。これは主に、マテリアルテクスチャの精度が不足していることが原因です。例えば、金属表面上に小さな（非金属）ダスト/砂のような粒子/スクラッチがある表面は、バイナリの金属値でレンダリングするのが困難です。

事前計算による F0F0誘電体と導体の両方で、両方のタイプの表面に同じフレネル・シュリック近似を使用できますが、金属表面がある場合は、ベースの反射率に色を付ける必要があります。通常、これは次のように行います。

vec3 F0 = vec3(0.04);

F0 = mix(F0, surfaceColor.rgb, metalness);

ほとんどの誘電体表面で近似される基本反射率を定義します。これはさらに別の近似ですF0F0最も一般的な誘電体を中心に平均化されます。0.04の基本反射率は、ほとんどの誘電体に当てはまり、追加の表面パラメーターを作成する必要なく、物理的に妥当な結果を生成します。次に、表面の金属度に基づいて、誘電体ベースの反射率を使用するか、F0F0表面の色として作成されました。金属表面はすべての屈折光を吸収するため、拡散反射はなく、表面の色テクスチャを基本反射率として直接使用できます。

コードでは、フレネルシュリック近似は次のように変換されます。

vec3 fresnelSchlick(float cosTheta, vec3 F0)

{

return F0 + (1.0 – F0) * pow(1.0 – cosTheta, 5.0);

}

cosTheta表面の法線との間のドット積の結果でありますんん そして途中 hh （または表示 vv）方向。

クックトーランス反射方程式

Cook-Torrance BRDFのすべてのコンポーネントについて説明したので、物理ベースのBRDFを現在の最終的な反射方程式に含めることができます。

ただし、この方程式は数学的に完全に正しいわけではありません。フレネル項はFF表面で反射される光の比率を表します。これは実質的に私たちの比率ですksks、つまり、反射方程式の鏡面反射（BRDF）部分に暗黙的に反射率が含まれている ksks。この場合、最終的な最終反射率の式は次のようになります。

この方程式は、物理ベースのレンダリングモデルを完全に記述します。物理ベースのレンダリングモデルは、物理ベースのレンダリング、つまりPBRとして一般的に理解されているものとして一般的に認識されています。議論されているすべての数学をコードにまとめる方法を完全に理解していなくても心配はいりません。次の章では、反射方程式を使用して、レンダリングされた照明でより物理的に妥当な結果を得る方法を探ります。すべてのビットとピースがゆっくりとはじまり始めます。

PBR資料の作成

PBRの基礎となる数学モデルの知識を使用して、アーティストがPBR方程式に直接フィードできるサーフェスの物理的特性を一般的にどのように作成するかを説明することで、議論を完成させます。PBRパイプラインに必要な各サーフェスパラメータは、テクスチャによって定義またはモデル化できます。テクスチャを使用すると、特定の各サーフェスポイントが光にどのように反応するかをフラグメントごとに制御できます。そのポイントが金属的であるか、粗いか滑らかか、またはサーフェスが異なる波長の光にどのように反応するかです。

以下は、PBRレンダラーに提供された場合の視覚的な出力とともに、PBRパイプラインで頻繁に見つかるテクスチャのリストです。

アルベド：アルベドテクスチャーは、各テクセルに対して表面の色、またはそのテクセルがメタリックの場合は基本反射率を指定します。これは以前に拡散テクスチャとして使用していたものとほぼ同じですが、すべての照明情報はテクスチャから抽出されます。多くの場合、拡散テクスチャには、画像内にわずかな影や暗い隙間があり、これはアルベドテクスチャでは望ましくないものです。表面の色（または屈折吸収係数）のみを含める必要があります。

法線：法線マップテクスチャは、法線マッピングの章でこれまで使用してきたものとまったく同じです。法線マップを使用すると、フラグメントごとに一意の法線を指定して、表面が対応する平面よりも凹凸があるように見せることができます。

メタリック：メタリックマップでは、テクセルがメタリックかそうでないかをテクセルごとに指定します。PBRエンジンの設定方法に基づいて、アーティストはメタルネスをグレースケール値またはバイナリの黒または白としてオーサリングできます。

粗さ：粗さマップは、テクセルごとにサーフェスの粗さを指定します。粗さのサンプリングされた粗さ値は、表面の統計的なマイクロファセットの向きに影響します。表面が粗いほど、反射は広くぼやけ、反射は滑らかになります。一部のPBRエンジンは、滑らかさ一部のアーティストがより直感的にわかるラフネスマップの代わりにマップ。これらの値は、1.0 – smoothnessサンプリングされた瞬間に粗度に変換されます（）。

AO：アンビエントオクルージョン または AOmapは、表面と周囲のジオメトリの潜在的なシャドウファクターを指定します。例えばレンガの表面がある場合、アルベドテクスチャはレンガの隙間の中にシャドウイング情報を持たないはずです。ただし、AOマップは、光が逃げるのがより難しいため、これらの暗いエッジを指定します。ライティングステージの最後にアンビエントオクルージョンを考慮すると、シーンの視覚的品質が大幅に向上します。メッシュ/サーフェスのアンビエントオクルージョンマップは、手動で生成されるか、3Dモデリングプログラムで事前に計算されます。

アーティストは、これらの物理ベースの入力値をテクセルごとに設定および調整し、テクスチャ値を実際のマテリアルの物理表面プロパティに基づいて設定できます。これはPBRレンダーパイプラインの最大の利点の1つです。環境や照明の設定に関係なく、サーフェスのこれらの物理プロパティは同じであり、アーティストが物理的にもっともらしい結果を得ることが容易になります。PBRパイプラインで作成されたサーフェスは、さまざまなPBRレンダリングエンジン間で簡単に共有でき、それらが置かれている環境に関係なく正しく見え、その結果、はるかに自然に見えます。

参考文献

コメントを残す

メールアドレスが公開されることはありません。

Next Post

PyOpenGLを使用したPBRレンダラー

金 7月 31 , 2020
https://www.artstation.com/artwork/4brXq8

You May Like